매끄러운 함수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

매끄러운 함수는 함수가 얼마나 여러 번 미분 가능한지를 나타내는 척도이며, 미분 가능성 클래스에 따라 분류된다. 함수가 k번 미분 가능하고 그 미분한 함수가 모두 연속일 경우 C^k 함수로 표기하며, 무한 번 미분 가능할 경우 C^∞, 해석 함수일 경우 C^ω로 표기한다. 매끄러운 함수는 무한히 미분 가능한 함수를 의미하며, 해석적이지 않은 매끄러운 함수도 존재한다. 매끄러운 함수는 매개변수 연속성(C^k)과 기하 연속성(Gⁿ)의 개념으로 곡선의 부드러움을 측정하는 데 사용되며, 건축, 디자인 등 다양한 분야에서 활용된다.

더 읽어볼만한 페이지

매끄러운 함수 - 분포 (해석학)
해석학에서 분포는 시험 함수 공간의 연속 쌍대 공간의 원소로 정의되며, 로랑 슈바르츠에 의해 정립되어 편미분 방정식의 해를 다루는 데 유용하고 미분 불가능하거나 특이점을 갖는 함수를 포함한 다양한 함수를 다루는 데 효과적인 일반적인 함수의 개념을 확장한 것이다.
매끄러운 함수 - 모스 이론
모스 이론은 미분다양체 위의 함수의 임계점과 지표를 이용하여 다양체의 위상수학적 성질을 연구하는 이론으로, 함수값에 따른 부분공간 변화를 관찰하여 다양체의 호몰로지를 계산하고 위상수학적 성질을 밝히는 데 응용된다.
해석학 (수학) - 수학적 최적화
수학적 최적화는 주어진 집합에서 실수 또는 정수 변수를 갖는 함수의 최댓값이나 최솟값을 찾는 문제로, 변수 종류, 제약 조건, 목적 함수 개수에 따라 다양한 분야로 나뉘며 여러 학문 분야에서 활용된다.
해석학 (수학) - 라플라스 변환
라플라스 변환은 함수 f(t)를 복소수 s를 사용하여 적분을 통해 다른 함수 F(s)로 변환하는 적분 변환이며, 선형성을 가지고 미분방정식 풀이 등 공학 분야에서 널리 사용된다.
대수기하학 - 타원곡선
타원곡선은 체 위에서 정의되고 특이점이 없으며 종수가 1인 사영 대수 곡선으로, 유리점을 가지며, 특정 형태의 방정식으로 표현되고, 실수체 위에서는 연결 성분 개수가 판별식에 따라 달라지며, 복소수체 위에서는 원환면과 위상적으로 동형이고, 점들 간에 군 연산이 정의되어 암호학 및 정수론에 활용된다.
대수기하학 - 크룰 차원
크룰 차원은 환 내의 소수 아이디얼 체인의 길이를 이용하여 정의되며, 환론 및 대수기하학에서 중요한 역할을 하고 다양한 개념으로 확장되어 사용된다.

매끄러운 함수

2. 미분가능성 클래스

미분 가능성 클래스는 함수의 도함수의 성질에 따라 함수를 분류하는 방법이다. 어떤 함수에 대해 존재하고 연속인 가장 높은 차수의 도함수를 측정하는 기준이 된다.

실수선 위의 열린 집합 $U$ 에서 실수값을 가지는 함수 $f$ 를 생각해보자. 음이 아닌 정수 ''k''에 대해, 함수 $f$ 의 도함수 $f', f'', \dots, f^{(k)}$ 가 존재하고 $U$ 에서 연속이면, $f$ 는 미분 가능성 '''클래스 '' $C^k$ '''''에 속한다. $f$ 가 $U$ 에서 $k$ 번 미분 가능하다면, $f', f'', \dots, f^{(k-1)}$ 은 $U$ 에서 연속이므로 적어도 클래스 $C^{k-1}$ 에 속한다.

함수 $f$ 가 $U$ 에서 모든 차수의 도함수를 가질 때 '''무한히 미분 가능''', '''매끄러운''', 또는 '''클래스 $C^\infty$ '''에 속한다고 한다. (따라서 이 모든 도함수는 $U$ 에서 연속 함수이다.)^[2] 함수 $f$ 가 '''클래스 $C^\omega$ ''' 또는 ''해석적''인 것은 $f$ 가 매끄럽고(즉, $C^\infty$ 에 속하며) 정의역 내의 임의의 점을 중심으로 한 테일러 급수 전개가 그 점의 어떤 근방에서 함수로 수렴하는 경우이다. 매끄럽지만 해석적이지 않은 함수가 존재하므로 $C^\omega$ 는 $C^\infty$ 에 엄밀하게 포함된다. 봉우리 함수는 이러한 성질을 가진 함수의 예이다.

다음 함수

f(x) = \begin{cases}x  & \mbox{if } x \geq 0, \\ 0 &\text{if } x < 0\end{cases}

는 연속이지만 x = 0에서 미분 불가능하므로, C⁰ 클래스에 속하지만 C¹ 클래스에는 속하지 않는다.

각 짝수 정수

k

에 대해 함수

f(x)=|x|^{k+1}

는 모든

x

에서 연속이고

k

번 미분 가능하다. 그러나

x = 0

에서는

f

가

(k + 1)

번 미분 가능하지 않으므로,

f

는 ''C''^$k$ 클래스에 속하지만

j > k

인 경우 ''C''^$j$ 클래스에는 속하지 않는다.

함수

g(x) = \begin{cases}x^2\sin{\left(\tfrac{1}{x}\right)} & x \neq 0일 때, \\ 0 & x = 0일 때\end{cases}

는 미분 가능하며, 도함수는

g'(x) = \begin{cases}-\mathord{\cos\left(\tfrac{1}{x}\right)} + 2x\sin\left(\tfrac{1}{x}\right) & x \neq 0일 때, \\ 0 & x = 0일 때\end{cases}

이다.

\cos(1/x)

가

x \to 0

일 때 진동하기 때문에,

g'(x)

는 0에서 연속이 아니다. 따라서

g(x)

는 미분 가능하지만 ''C''¹급이 아니다.

함수의 정의역이

X

일 때 그것을 명시하여,

X

위에서 정의되는

C^k

급 함수 전체가 이루는 공간을 종종

C^k(X)

와 같이 표기한다. 정의역

X

는 많은 경우 "매끄러운" 위상 공간이다. 더 나아가 치역

Y

를 명시하여

C^k(X; Y)

등으로 표기하기도 한다. 치역

Y

는 이 공간의 계수로 간주된다.

함수 ''f''가 (그 함수가 속한 문맥에서 논의하는 데 사용하기에) 충분히 큰 ''n''에 대해 ''C''^''n''-급일 때, '''매끄러운 함수'''라고 총칭한다. 이때, 함수 ''f''는 '''충분히 매끄럽다'''고도 한다. 이러한 용어를 사용할 때, ''n''은 충분히 크면 되고, 그 값이 정확히 알려져 있을 필요는 없으며, 특히 ''n''을 고정해서 생각하지 않는 것이 일반적이다.

매끄러움의 개념은 (미분의 개념이 그러하듯이) 국소적인 것이다. 즉, 어떤 점에서의 매끄러움이란 그 점 주위의 충분히 작은 근방에서 고찰된다. 유한 개의 예외를 제외한 각 점에서 매끄러운 함수는 '''구간별로 매끄럽다'''고 한다.

2. 1. C^k 함수

어떤 함수가 k번 미분가능하고 그 미분한 함수가 모두 연속일 경우, 그 함수를 C^k 함수라고 부른다. 예를 들어, C⁰는 연속인 함수를 의미하며, C¹는 '''연속 미분 가능한 함수''', 즉 미분 가능하고 도함수가 연속 함수인 함수를 의미한다.^[2]

일반적으로, 자연수 k에 대해, f의 k계 도함수가 존재하고 연속일 때, f는 k '''계 연속적으로 미분 가능'''하다고 하며, f는 C^k급 함수라고 한다. 미분 가능한 함수는 연속이므로, C^k (k = 1, 2, ...)는 포함 관계에 관하여 비증가하는 수열을 이룬다. 임의 유한 계의 도함수를 갖는 함수는 '''무한 계'''(연속적)'''미분 가능'''하다고 하며, 그 클래스는 C^∞로 표시된다.^[2]

함수가 무한 번 미분가능할 경우 C^∞로 표기하며, 해석 함수일 경우는 C^ω로 표기한다.^[2]

C^k 집합은 C^k+1 집합을 진부분집합으로 가지며, C^k+1에 속하지 않는 C^k 함수가 존재한다. 마찬가지로 C^k는 C^∞를 진부분집합으로, C^∞는 C^ω를 진부분집합으로 가진다.^[2]

2. 2. C^∞ 함수

어떤 함수가 무한 번 미분 가능할 경우

C^\infty

로 표기하며, 이러한 함수를 매끄러운 함수라고 부른다.^[2] 봉우리 함수는 매끄럽지만 해석 함수는 아닌 함수의 예시이다.

함수가 '''연속적으로 미분 가능'''(continuously differentiable)하다는 것은 도함수가 존재하고, 그 도함수가 연속 함수가 되는 것을 의미한다.

마찬가지로 자연수 k에 대해, f의 k계 도함수가 존재하고 연속일 때, f는 '''k계 연속적으로 미분 가능'''하다고 하며, 또한 f는 C^k급 함수라고 한다. 미분 가능한 함수는 연속이므로, C^k (k = 1, 2, ...)는 포함 관계에 관하여 비증가하는 수열을 이룬다. 임의 유한 계의 도함수를 갖는 함수는 '''무한 계'''(연속적)'''미분 가능'''하다고 하며, 그 클래스는 ''C''^∞로 표시된다.

더 강한 매끄러움을 나타내는 클래스로, 각 점에서 멱급수 전개가 가능한 함수의 클래스인 해석 함수 C^ω가 있다. 경우에 따라, 연속 함수의 클래스 C를 0계 연속적으로 미분 가능한 함수의 클래스 C⁰로 생각하여, 매끄러운 함수의 범주에 포함시키기도 한다.

함수 ''f''가 (그 함수가 속한 문맥에서 논의하는 데 사용하기에) 충분히 큰 ''n''에 대해 ''C''^''n''급일 때, '''매끄러운 함수'''(smooth function)라고 총칭한다. 이때, 함수 ''f''는 '''충분히 매끄럽다'''고도 한다.

그러한 상황에서는 대부분, 「매끄러운 함수」의 클래스로서 무한히 미분 가능한 함수의 클래스 ''C''^∞나 해석 함수의 클래스 ''C''^ω를 생각하는 것이 논의의 편의를 위해 유용하다.

2. 3. C^ω 함수

함수가 해석 함수일 경우

C^\omega

로 표기한다. 해석 함수는 테일러 급수로 전개 가능한 함수를 의미하며, 모든

C^\omega

함수는

C^\infty

함수이지만, 그 역은 성립하지 않는다.^[2] 지수 함수

e^{x}

는 해석적이므로

C^\omega

에 속한다. 삼각 함수들 또한 정의된 곳 어디에서든 해석적이다. 왜냐하면 그것들은 복소 지수 함수

e^{ix}

와

e^{-ix}

의 선형 결합이기 때문이다. 봉우리 함수는 매끄럽지만,

C^\omega

클래스에는 속하지 않는 함수의 예시이다.

2. 4. 포함 관계

C^k^영어 집합은 C^(k+1)^영어 집합을 진부분집합으로 가지며, C^(k+1)^영어에 속하지 않는 C^k^영어 함수가 존재한다. 마찬가지로 C^k^영어는 C^∞^영어를 진부분집합으로, C^∞^영어는 C^ω^영어를 진부분집합으로 가진다.^[2]

3. 예시

$C^0$ 이지만 $C^1$ 은 아닌 함수의 예시는 하위 섹션을 참고.
$C^∞$ 이지만 $C^ω$ 가 아닌 함수의 예시는 하위 섹션을 참고.

다음 함수는 미분 가능하지만, 연속적으로 미분 가능하지 않다.

g(x) = \begin{cases}x^2\sin{\left(\tfrac{1}{x}\right)} & x \neq 0일 때, \\ 0 & x = 0일 때\end{cases}

이 함수의 도함수는 다음과 같다.

g'(x) = \begin{cases}-\mathord{\cos\left(\tfrac{1}{x}\right)} + 2x\sin\left(\tfrac{1}{x}\right) & x \neq 0일 때, \\ 0 & x = 0일 때\end{cases}

\cos(1/x)

가 0으로 수렴할 때 진동하기 때문에,

g'(x)

는 0에서 연속이 아니다. 따라서

g(x)

는 미분 가능하지만

C^1

급이 아니다.

지수 함수

e^{x}

는 해석 함수이므로

C^ω

에 속한다. 삼각 함수들 또한 정의된 곳 어디에서든 해석적인데, 이는 복소 지수 함수

e^{ix}

와

e^{-ix}

의 선형 결합이기 때문이다.

3. 1. C^0이지만 C^1이 아닌 함수

f(x)

가

x

가 0 이상일 때

f(x) = x

, 0보다 작을 때

f(x) = 0

인 경우, 이 함수는 연속함수이지만

x=0

에서 미분값이 존재하지 않는다. 따라서 이 함수는

C^0

이지만

C^1

은 아니다.

다음 함수도 마찬가지로 C⁰이지만 C¹은 아니다.

f(x) = \begin{cases}x  & \mbox{if } x \geq 0, \\ 0 &\text{if } x < 0\end{cases}

3. 2. C^k이지만 C^(k+1)이 아닌 함수

각 짝수 정수 k에 대해 함수

f(x)=|x|^{k+1}

는 모든 x에서 연속이고 k번 미분 가능하다. 그러나 x = 0 에서는 f가 (k + 1)번 미분 가능하지 않으므로, f는 C^k 클래스에 속하지만 j > k인 경우 C^j 클래스에는 속하지 않는다.

3. 3. C^∞이지만 C^ω가 아닌 함수

:

f(x) = \begin{cases}e^{-1/(1-x^2)} & \mbox{ if } |x| < 1, \\ 0 &\mbox{ otherwise }\end{cases}

인 함수는 무한 번 미분이 가능하므로 매끄러운 함수이다. 하지만

x = \pm 1

일 때 해석적이지 않고, 따라서 이 함수는 해석함수가 아니다.

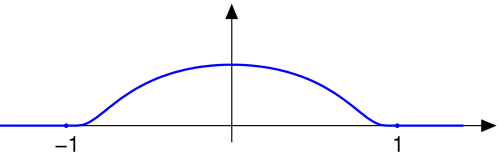
봉우리 함수

:

f(x) = \begin{cases}e^{-\frac{1}{1-x^2}} & \text{ if } |x| < 1, \\ 0 &\text{ otherwise }\end{cases}

는 매끄럽고, 따라서 ''C''^∞ 클래스에 속하지만,

x=\pm 1

에서 해석적이지 않으며, 따라서 ''C''^ω 클래스에는 속하지 않는다. 함수 f는 컴팩트 지지집합을 갖는 매끄러운 함수의 예이다.

4. 성질

C^∞^영어 함수 공간은 프레셰 공간의 구조를 가진다. 이는 반노름을 사용하여 정의할 수 있다. 이러한 공간은 특정 차수의 도함수를 갖는 함수가 필요한 응용 분야에서 자연스럽게 나타나지만, 특히 편미분 방정식 연구에서는 소볼레프 공간을 사용하는 것이 더 유익할 수 있다.^[1]

4. 1. 프레셰 공간

Fréchet space^영어 공간은 반노름을 사용하여 정의할 수 있다. 유클리드 공간의 열린 집합

U\subset\mathbb R^n

에 대하여,

\mathcal C^\infty(U;\mathbb R)

가

U

위의 매끄러운 실수값 함수들의 집합이라고 하자.

이 공간 위에는 다음과 같은 일련의 반노름들이 주어진다. 모든 콤팩트 공간

K\subset U

및 다중 지표

\alpha\in\mathbb N^n

에 대하여, 다음과 같이 정의된다.

:

\|f\|_{K,\alpha}=\sup_K|\partial^\alpha f|

따라서, 이 반노름들을 사용하여

\mathcal C^\infty(U;\mathbb R)

위에 프레셰 공간의 구조를 줄 수 있다.

D

를 실수선의 열린 부분집합이라고 하자.

D

위에 정의된 모든

C^k

실수값 함수들의 집합은 다음과 같은 가산 개의 반노름으로 프레셰 벡터 공간을 이룬다.

p_{K, m}=\sup_{x\in K}\left|f^{(m)}(x)\right|

여기서

K

는 그 합집합이

D

인 증가하는 컴팩트 집합들의 수열을 나타내고,

m=0,1,\dots,k

이다.

D

위의

C^\infty

함수들의 집합 또한 프레셰 공간을 이룬다. 위와 같은 반노름을 사용하지만,

m

은 모든 음이 아닌 정수값을 가질 수 있다.

5. 다변수 함수의 미분가능성 클래스

다변수 함수의 미분가능성 클래스는 편미분과 프레셰 미분을 이용하여 정의한다. 함수가 연속적으로 미분 가능하다는 것은 함수의 도함수가 존재하고, 그 도함수가 연속 함수임을 의미한다.

자연수 k에 대해, f의 k계 도함수가 존재하고 연속일 때, f는 k번 연속적으로 미분 가능하다고 하며, C^k급 함수라고 한다. 미분 가능한 함수는 연속이므로, C^k (k = 1, 2, ...)는 포함 관계에 따라 감소하는 수열을 이룬다. 임의 유한 번 미분 가능한 함수는 무한 번 (연속적) 미분 가능하다고 하며, 그 클래스는 C^∞로 표시된다.

이보다 더 강한 매끄러움을 나타내는 클래스로, 각 점에서 멱급수 전개가 가능한 함수의 클래스인 해석 함수 C^ω가 있다. 경우에 따라, 연속 함수의 클래스 C를 0번 연속적으로 미분 가능한 함수의 클래스 C⁰로 보아, 매끄러운 함수의 범주에 포함시키기도 한다.

매끄러움의 클래스는 구체적인 정의역과 치역을 부여함으로써, 많은 함수 공간의 예시를 제공한다. 함수의 정의역이 X일 때, X 위에서 정의되는 C^k급 함수 전체가 이루는 공간을 종종 C^k(X)와 같이 표기한다. 정의역 X는 "매끄러운" 위상 공간인 경우가 많다. 치역 Y를 명시하여 C^k(X; Y) 등으로 표기하기도 하며, 치역 Y는 이 공간의 계수로 간주된다.

5. 1. C^k 함수 (다변수)

열린 집합 U⊂ℝⁿ에서 ℝ로 정의된 함수 f:U⊂ℝⁿ→ℝ는 양의 정수 k에 대해 U에서 C^k 클래스라고 한다.^[3] 모든 편미분

\frac{\partial^\alpha f}{\partial x_1^{\alpha_1} \, \partial x_2^{\alpha_2}\,\cdots\,\partial x_n^{\alpha_n}}(y_1,y_2,\ldots,y_n)

이 존재하고 연속이라면, 여기서 α₁,α₂,…,αⁿ은 α=α₁+α₂+⋯+αⁿ≤k인 모든 음이 아닌 정수이고, 모든 (y₁,y₂,…,yⁿ)∈U이다. 동등하게, f가 U에서 k계 프레셰 미분이 존재하고 U의 모든 점에서 연속이라면 f는 U에서 C^k 클래스이다. 함수 f는 U에서 연속이라면 C 또는 C⁰ 클래스라고 한다. C¹ 클래스의 함수는 '연속적으로 미분 가능하다'라고도 한다.

열린 집합 U⊂ℝⁿ에서 ℝ^m로 정의된 함수 f:U⊂ℝⁿ→ℝ^m는 양의 정수 k에 대해 U에서 C^k 클래스라고 한다. 만약 그것의 모든 성분

f_i(x_1,x_2,\ldots,x_n)=(\pi_i\circ f)(x_1,x_2,\ldots,x_n)=\pi_i(f(x_1,x_2,\ldots,x_n)) \text{ for } i=1,2,3,\ldots,m

이 C^k 클래스라면, 여기서 πᵢ는 πᵢ:ℝ^m→ℝ로 정의된 자연스러운 사영 πᵢ(x₁,x₂,…,x_m)=xᵢ이다. 만약 연속이거나, 동등하게 모든 성분 fᵢ가 U에서 연속이라면 C 또는 C⁰ 클래스라고 한다.

6. 매개변수 연속성과 기하 연속성

브라이언 바스키는 매개변수 연속성(''C''^''k'') 및 기하 연속성(Gⁿ)이라는 용어를 도입하여 곡선의 부드러움을 측정할 수 있음을 보여주었다.^[4]^[5]^[6] 매개변수 연속성은 매개변수 곡선에 적용되는 개념으로, 곡선을 따라 거리에 대한 매개변수 값의 부드러움을 설명한다. 기하 연속성은 곡선이나 곡면의 매끄러움 정도를 나타낸다.

일반적으로 Gⁿ 연속성은 곡선을 다시 매개변수화하여 Cⁿ 연속성을 갖도록 할 수 있다면 존재한다.^[8]^[9] 마찬가지로, $f(1)=g(0)$ 인 두 벡터 함수 $f(t)$ 와 $g(t)$ 가 만나는 점에서 베타 제약 조건으로 알려진 방정식을 만족하는 경우 Gⁿ 연속성을 갖는다.

6. 1. 매개변수 연속성 (C^k)

브라이언 바스키는 매개변수 연속성(''C''^''k'') 및 기하 연속성(Gⁿ)이라는 용어를 도입하여, 매개변수가 곡선을 따라가는 속도에 대한 제약을 제거함으로써 곡선의 부드러움을 측정할 수 있음을 보여주었다.^[4]^[5]^[6]

매개변수 연속성(''C''^''k'')은 매개변수 곡선에 적용되는 개념으로, 곡선을 따라 거리에 대한 매개변수 값의 부드러움을 설명한다. 매개변수 곡선

s:[0,1]\to\mathbb{R}^n

은

\textstyle \frac{d^ks}{dt^k}

가 존재하고

[0,1]

에서 연속일 때 ''C''^''k'' 클래스라고 한다. 여기서 끝점

0

과

1

에서의 도함수는 일방 도함수(

0

에서는 오른쪽에서,

1

에서는 왼쪽에서)로 간주한다.

시간 매개변수를 갖는 물체의 운동을 설명하는 곡선은 물체가 유한한 가속도를 갖도록 ''C''¹ 연속성을 가져야 하고, 그 1차 도함수는 미분 가능해야 한다. 영화 제작 중 카메라 경로와 같이 더 부드러운 움직임을 위해서는 더 높은 차수의 매개변수 연속성이 필요하다.

매개변수 연속성의 여러 차수는 다음과 같이 설명할 수 있다.^[7]

$C^0$ : 0차 도함수가 연속(곡선이 연속)
$C^1$ : 0차 및 1차 도함수가 연속
$C^2$ : 0차, 1차 및 2차 도함수가 연속
$C^n$ : 0차부터 $n$ 차까지의 도함수가 연속

6. 2. 기하 연속성 (G^n)

G² 연속성을 갖는 이차곡선의 족: p는 고정,

\varepsilon

는 변수 (

\varepsilon=0

: 원,

\varepsilon=0.8

: 타원,

\varepsilon=1

: 포물선,

\varepsilon=1.2

: 쌍곡선)

곡선 또는 곡면은 매끄러움의 정도를 나타내는 n을 사용하여 Gⁿ 연속성을 갖는다고 설명할 수 있다. 곡선 상의 한 점의 양쪽에 있는 선분을 고려하면 다음과 같다.

G⁰: 곡선은 연결점에서 만난다.
G¹: 곡선은 연결점에서 공통 접선 방향을 공유한다.
G²: 곡선은 연결점에서 공통 곡률 중심을 공유한다.

일반적으로, 곡선을 다시 매개변수화하여 Cⁿ(매개변수) 연속성을 갖도록 할 수 있다면 Gⁿ 연속성이 존재한다.^[8]^[9] 곡선의 재매개변수화는 원래 곡선과 기하학적으로 동일하며 매개변수만 영향을 받는다.

마찬가지로,

f(1)=g(0)

인 두 벡터 함수

f(t)

와

g(t)

는 만나는 점에서 베타 제약 조건으로 알려진 방정식을 만족하는 경우 Gⁿ 연속성을 갖는다.

곡선이 매끄럽게 보이려면 G¹ 연속성이 필요하지만, 건축 및 스포츠카 디자인에서 추구하는 것과 같은 좋은 미학을 위해서는 더 높은 수준의 기하 연속성이 필요하다. 예를 들어, 자동차 차체의 반사는 차체가 G² 연속성을 갖지 않으면 매끄럽게 보이지 않는다.

(네 모서리에 90도 원호가 있는)은 G¹ 연속성을 갖지만 G² 연속성을 갖지 않는다. 모서리에 구의 8분원과 모서리를 따라 4분원 기둥이 있는 경우도 마찬가지이다. G² 연속성을 갖는 편집 가능한 곡선이 필요한 경우 일반적으로 3차 스플라인을 선택한다. 이러한 곡선은 산업 디자인에서 자주 사용된다.

7. 다른 개념과의 관계

해석 함수는 해석적인 집합에서 "매끄러운" 함수이지만, 충격 함수와 같은 예는 실수 함수의 경우 그 역이 성립하지 않음을 보여준다. 즉, 해석적이지 않은 매끄러운 실수 함수가 존재한다.^[1] 어떤 점에서도 매끄럽지만 해석적이지 않은 함수의 간단한 예로 푸리에 급수나 파비우스 함수가 있다.^[1] 이러한 함수들이 예외적인 것처럼 보일 수 있지만, 매끄러운 함수들 중 해석 함수는 매우 드물게 분포한다.^[1] 더 엄밀하게 말하면, 해석 함수는 매끄러운 함수 집합에서 희소 집합을 형성한다.^[1]

이 상황은 실수선에서 초월수의 편재성과 비교할 수 있다.^[1] 실수선과 매끄러운 함수 집합 모두에서, 우리가 처음 떠올리는 예(대수적/유리수와 해석 함수)는 대부분의 경우보다 훨씬 더 잘 정의되어 있다.^[1] 초월수와 어디에서도 해석적이지 않은 함수는 풀 측도(여집합은 희소)를 가진다.^[1]

이는 복소 미분 가능 함수와 현저히 대조된다.^[1] 열린 집합에서 복소 함수가 한 번만 미분 가능하면, 그 집합에서 무한히 미분 가능하고 해석적이다.

지지집합(support)이 주어진 매끄러운 함수는 '''매끄러운 분할 단위'''(분할 단위 및 위상 용어집 참조)를 구성하는 데 사용되며, 이는 매끄러운 다양체 연구에 필수적이다.^[1] 간단한 예로 실수 직선상의 범프 함수가 있다.^[1] 즉, 구간 [a, b] 외부에서는 값이 0이고, a < x < b일 때 f(x) > 0을 만족하는 매끄러운 함수 f이다.

직선상의 여러 겹치는 구간이 주어지면 각 구간과 반무한 구간 $(-\infty, c]$ 및 $[d, +\infty)$ 에 대해 범프 함수를 구성하여 전체 직선을 덮을 수 있으며, 함수들의 합은 항상 1이 된다.^[1]

분할 단위는 정칙 함수에는 적용되지 않는다.^[1] 존재와 해석적 연속에 대한 서로 다른 거동은 층 이론의 근본 중 하나이다.^[1] 반대로, 매끄러운 함수의 층은 위상 정보를 거의 담고 있지 않다.^[1]

7. 1. 해석 함수와의 관계

지수 함수

e^{x}

와 삼각 함수는 정의된 곳 어디에서든 해석적이므로 매끄러운 함수이다. 봉우리 함수의 일종인

f(x) = \begin{cases}e^{-\frac{1}{1-x^2}} & \text{ if } |x| < 1, \\ 0 &\text{ otherwise }\end{cases}

는 매끄러운 함수이지만,

x = \pm 1

에서 해석적이지 않다. 이 함수는 콤팩트 지지 집합을 갖는 매끄러운 함수의 예시이다.

모든 해석 함수는 매끄러운 함수이지만, 위에서 언급된 충격 함수와 같은 예시는 그 역이 성립하지 않음을 보여준다. 즉, 해석적이지 않은 매끄러운 함수가 존재한다. 어떤 점에서도 매끄럽지만 해석적이지 않은 함수의 예시는 푸리에 급수나 파비우스 함수를 통해 만들 수 있다.

매끄러운 함수들 중에서 해석 함수는 매우 드물게 분포하며, 해석 함수들은 매끄러운 함수들의 집합에서 희소 집합을 형성한다.

7. 2. 정칙 함수와의 관계

지지집합(support)이 주어진 매끄러운 함수는 '''매끄러운 분할 단위'''(분할 단위 및 위상 용어집 참조)를 구성하는 데 사용되며, 이는 매끄러운 다양체 연구에 필수적이다. 간단한 예로 실수 직선상의 범프 함수가 있다.

분할 단위는 정칙 함수에는 적용되지 않는다. 존재와 해석적 연속에 대한 서로 다른 거동은 층 이론의 근본 중 하나이다. 반대로, 매끄러운 함수의 층은 위상 정보를 거의 담고 있지 않다.

참조

_[1] 웹사이트 Smooth Function http://mathworld.wol[...] 2019-12-13
_[2] 서적 Foundations of Differentiable Manifolds and Lie Groups https://books.google[...] Springer 2014-11-28
_[3] 서적 Cours de calcul différentiel Paris: Hermann
_[4] Ph.D. The Beta-spline: A Local Representation Based on Shape Parameters and Fundamental Geometric Measures https://dl.acm.org/c[...] University of Utah, Salt Lake City, Utah 1981
_[5] 서적 Computer Graphics and Geometric Modeling Using Beta-splines Springer-Verlag, Heidelberg
_[6] 서적 An Introduction to Splines for Use in Computer Graphics and Geometric Modeling Morgan Kaufmann
_[7] 웹사이트 Parametric Curves https://www.cs.helsi[...] University of Toronto, Canada 1996
_[8] 학술지 Geometric Continuity of Parametric Curves: Three Equivalent Characterizations
_[9] 웹사이트 Geometry and Algorithms for Computer Aided Design https://www2.mathema[...] Technische Universität Darmstadt 2003
_[10] 서적 Differential Topology Prentice-Hall

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com